13.10.2019
Τιμές πίνακα sin cos tg ctg. Τριγωνομετρικές συναρτήσεις
Στο άρθρο, θα καταλάβουμε πλήρως πώς μοιάζει πίνακας τριγωνομετρικών τιμών, ημιτόνου, συνημίτονος, εφαπτομένης και συνεφαπτομένης. Εξετάστε την κύρια τιμή τριγωνομετρικές συναρτήσεις, από γωνία 0,30,45,60,90,...,360 μοιρών. Και ας δούμε πώς να χρησιμοποιήσουμε αυτούς τους πίνακες για τον υπολογισμό της τιμής των τριγωνομετρικών συναρτήσεων.
Πρώτα σκεφτείτε πίνακας συνημιτόνου, ημιτόνου, εφαπτομένης και συνεφαπτομένηςαπό γωνία 0, 30, 45, 60, 90,... μοιρών. Ο ορισμός αυτών των μεγεθών καθιστά δυνατό τον προσδιορισμό της τιμής των συναρτήσεων των γωνιών 0 και 90 μοιρών:
sin 0 0 \u003d 0, cos 0 0 \u003d 1. tg 00 \u003d 0, η συνεφαπτομένη του 00 θα είναι απροσδιόριστη
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, η εφαπτομένη του 90 0 θα είναι απροσδιόριστη
Αν πάρουμε ορθογώνια τρίγωνα των οποίων οι γωνίες είναι από 30 έως 90 μοίρες. Παίρνουμε:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
αμαρτία 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
αμαρτία 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, ctg 60 0 = √3/3
Αντιπροσωπεύουμε όλες τις λαμβανόμενες τιμές στη φόρμα τριγωνομετρικός πίνακας:
Πίνακας ημιτόνων, συνημιτόνων, εφαπτομένων και συνεφαπτομένων!
Εάν χρησιμοποιήσουμε τη φόρμουλα χυτού, ο πίνακας μας θα αυξηθεί, θα προστεθούν τιμές για γωνίες έως 360 μοίρες. Θα μοιάζει με:

Επίσης, με βάση τις ιδιότητες της περιοδικότητας, ο πίνακας μπορεί να αυξηθεί αν αντικαταστήσουμε τις γωνίες με 0 0 +360 0 *z .... 330 0 +360 0 *z, όπου το z είναι ακέραιος. Σε αυτόν τον πίνακα, είναι δυνατός ο υπολογισμός της τιμής όλων των γωνιών που αντιστοιχούν σε σημεία ενός μόνο κύκλου.

Ας δούμε ξεκάθαρα πώς να χρησιμοποιήσετε τον πίνακα στη λύση.
Όλα είναι πολύ απλά. Επειδή η τιμή που χρειαζόμαστε βρίσκεται στο σημείο τομής των κελιών που χρειαζόμαστε. Για παράδειγμα, ας πάρουμε το cos μιας γωνίας 60 μοιρών, στον πίνακα θα μοιάζει με αυτό:

Στον τελικό πίνακα των κύριων τιμών των τριγωνομετρικών συναρτήσεων ενεργούμε με τον ίδιο τρόπο. Αλλά σε αυτόν τον πίνακα είναι δυνατό να μάθουμε πόση θα είναι η εφαπτομένη από γωνία 1020 μοιρών, = -√3 Ας ελέγξουμε 1020 0 = 300 0 +360 0 *2. Ας βρούμε το τραπέζι.

Τραπέζι Bradis. Για ημίτονο, συνημίτονο, εφαπτομένη και συνεφαπτομένη.
Οι πίνακες του Bradys χωρίζονται σε διάφορα μέρη, αποτελούνται από πίνακες συνημιτόνου και ημιτόνου, εφαπτομένης και συνεφαπτομένης - που χωρίζεται σε δύο μέρη (tg γωνίας έως 90 μοίρες και ctg μικρών γωνιών).
Ημίτονο και συνημίτονο

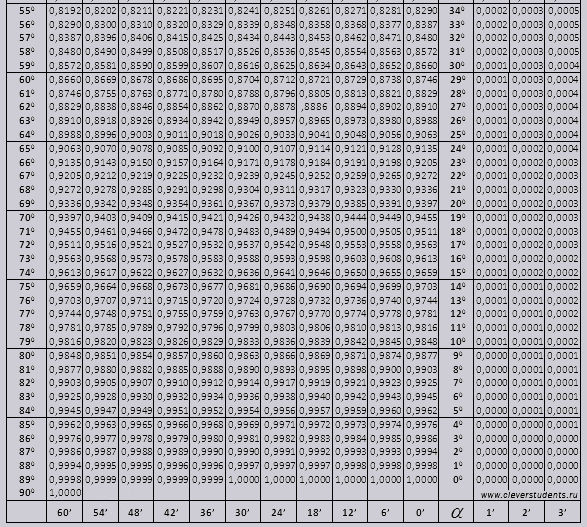
γωνία tg από 00 έως 760, γωνία ctg από 140 έως 900.

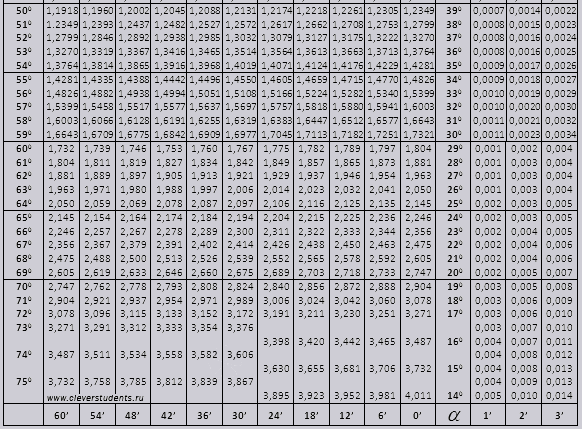
tg έως 900 και ctg μικρές γωνίες.

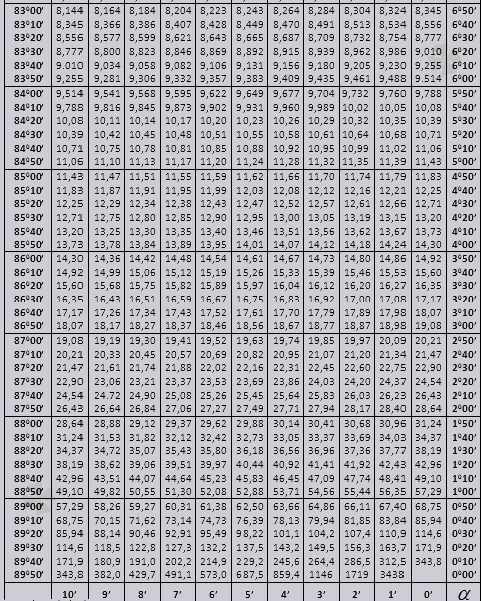
Ας μάθουμε πώς να χρησιμοποιήσουμε τους πίνακες Bradis στην επίλυση προβλημάτων.
Ας βρούμε τον προσδιορισμό sin (ο χαρακτηρισμός στη στήλη από την αριστερή άκρη) 42 λεπτά (ο χαρακτηρισμός βρίσκεται στην επάνω γραμμή). Διασταυρώνοντας αναζητούμε προσδιορισμό, είναι = 0,3040.
Οι τιμές των λεπτών υποδεικνύονται με ένα διάστημα έξι λεπτών, τι γίνεται αν η τιμή που χρειαζόμαστε εμπίπτει σε αυτό το διάστημα. Ας πάρουμε 44 λεπτά και υπάρχουν μόνο 42 στον πίνακα. Λαμβάνουμε ως βάση τα 42 και χρησιμοποιούμε πρόσθετες στήλες στο σωστη πλευρα, παίρνουμε τη 2η τροποποίηση και προσθέτουμε στο 0,3040 + 0,0006 παίρνουμε 0,3046.
Με αμαρτία 47 λεπτά, παίρνουμε ως βάση 48 λεπτά και αφαιρούμε 1 διόρθωση από αυτό, δηλαδή 0,3057 - 0,0003 = 0,3054
Κατά τον υπολογισμό του cos, εργαζόμαστε παρόμοια με το sin, μόνο που παίρνουμε ως βάση την κάτω σειρά του πίνακα. Για παράδειγμα cos 20 0 = 0,9397
Οι τιμές tg γωνίας έως 90 0 και βρεφικής κούνιας μικρής γωνίας είναι σωστές και δεν υπάρχουν διορθώσεις σε αυτές. Για παράδειγμα, βρείτε tg 78 0 37min = 4,967 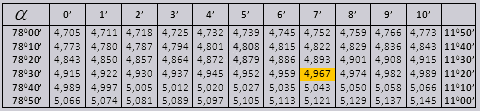
και ctg 20 0 13 min = 25,83 
Λοιπόν, εδώ εξετάσαμε τους κύριους τριγωνομετρικούς πίνακες. Ελπίζουμε ότι αυτές οι πληροφορίες ήταν εξαιρετικά χρήσιμες για εσάς. Οι ερωτήσεις σας στα τραπέζια, αν υπάρχουν, γράψτε οπωσδήποτε στα σχόλια!
Σημείωση: Φτερά τοίχου - μια σανίδα φτερού για την προστασία των τοίχων. Ακολουθήστε τον σύνδεσμο φτερά χωρίς πλαίσιο χωρίς πλαίσιο (http://www.spi-polymer.ru/otboyniki/) και μάθετε περισσότερα.
Πίνακας βασικών τριγωνομετρικών συναρτήσεων για γωνίες 0, 30, 45, 60, 90, ... μοίρες
Από τους τριγωνομετρικούς ορισμούς των συναρτήσεων $\sin$, $\cos$, $\tan$ και $\cot$, μπορεί κανείς να βρει τις τιμές τους για τις γωνίες $0$ και $90$ μοίρες:
$\sin0°=0$, $\cos0°=1$, $\tan 0°=0$, $\cot 0°$ δεν έχει οριστεί.
$\sin90°=1$, $\cos90°=0$, $\cot90°=0$, $\tan 90°$ δεν έχει οριστεί.
Στο μάθημα της σχολικής γεωμετρίας, όταν μελετάμε ορθογώνια τρίγωνα, βρίσκονται οι τριγωνομετρικές συναρτήσεις των γωνιών $0°$, $30°$, $45°$, $60°$ και $90°$.
Οι τιμές που βρέθηκαν των τριγωνομετρικών συναρτήσεων για τις καθορισμένες γωνίες σε μοίρες και ακτίνια αντίστοιχα ($0$, $\frac(\pi)(6)$, $\frac(\pi)(4)$, $\frac(\ pi)(3) $, $\frac(\pi)(2)$) για ευκολία απομνημόνευσης και χρήσης εισάγονται σε έναν πίνακα που ονομάζεται τριγωνομετρικός πίνακας, πίνακας βασικών τιμών τριγωνομετρικών συναρτήσεωνκαι τα λοιπά.
Όταν χρησιμοποιείτε τύπους μείωσης, τριγωνομετρικός πίνακαςμπορεί να επεκταθεί σε $360°$ και $2\pi$ ακτίνια αντίστοιχα:
Εφαρμόζοντας τις ιδιότητες περιοδικότητας των τριγωνομετρικών συναρτήσεων, κάθε γωνία που διαφέρει από την ήδη γνωστή κατά $360°$ μπορεί να υπολογιστεί και να καταγραφεί σε έναν πίνακα. Για παράδειγμα, η τριγωνομετρική συνάρτηση για τη γωνία $0°$ θα έχει την ίδια τιμή για τη γωνία $0°+360°$ και για τη γωνία $0°+2 \cdot 360°$ και για τη γωνία $0°+3 \ cdot 360°$ κ.λπ.
Χρησιμοποιώντας έναν τριγωνομετρικό πίνακα, μπορείτε να προσδιορίσετε τις τιμές όλων των γωνιών ενός κύκλου μονάδας.
Στο μάθημα της σχολικής γεωμετρίας, υποτίθεται ότι απομνημονεύει τις βασικές τιμές των τριγωνομετρικών συναρτήσεων που συλλέγονται σε έναν τριγωνομετρικό πίνακα για την ευκολία επίλυσης τριγωνομετρικών προβλημάτων.
Χρησιμοποιώντας έναν πίνακα
Στον πίνακα, αρκεί να βρούμε την απαραίτητη τριγωνομετρική συνάρτηση και την τιμή της γωνίας ή του ακτινίου για την οποία πρέπει να υπολογιστεί αυτή η συνάρτηση. Στην τομή της γραμμής με τη συνάρτηση και της στήλης με την τιμή, παίρνουμε την επιθυμητή τιμή της τριγωνομετρικής συνάρτησης του δεδομένου ορίσματος.
Στο σχήμα μπορείτε να δείτε πώς να βρείτε την τιμή $\cos60°$ που ισούται με $\frac(1)(2)$.
Ο διευρυμένος τριγωνομετρικός πίνακας χρησιμοποιείται με παρόμοιο τρόπο. Το πλεονέκτημα της χρήσης του είναι, όπως ήδη αναφέρθηκε, ο υπολογισμός της τριγωνομετρικής συνάρτησης σχεδόν κάθε γωνίας. Για παράδειγμα, μπορείτε εύκολα να βρείτε την τιμή $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300 °$:
Πίνακες Bradis βασικών τριγωνομετρικών συναρτήσεων
Η δυνατότητα υπολογισμού της τριγωνομετρικής συνάρτησης απολύτως οποιασδήποτε τιμής γωνίας για μια ακέραια τιμή μοιρών και μια ακέραια τιμή των λεπτών δίνει τη χρήση των πινάκων Bradis. Για παράδειγμα, βρείτε την τιμή $\cos34°7"$. Οι πίνακες χωρίζονται σε 2 μέρη: τον πίνακα των τιμών $\sin$ και $\cos$ και τον πίνακα των $\tan$ και $\ τιμές κούνιας.
Οι πίνακες Bradis καθιστούν δυνατή τη λήψη μιας κατά προσέγγιση τιμής τριγωνομετρικών συναρτήσεων με ακρίβεια έως και 4 δεκαδικών ψηφίων.
Χρήση πινάκων Bradis
Χρησιμοποιώντας τους πίνακες του Bradys για ημίτονο, βρίσκουμε $\sin17°42"$. Για να το κάνετε αυτό, στη στήλη στα αριστερά του πίνακα ημιτόνων και συνημιτόνων βρίσκουμε την τιμή των μοιρών - $17°$, και σε στην επάνω γραμμή βρίσκουμε την τιμή των λεπτών - $42"$. Στη διασταύρωση τους, παίρνουμε την επιθυμητή τιμή:
$\sin17°42"=0,304$.
Για να βρείτε την τιμή του $\sin17°44"$, πρέπει να χρησιμοποιήσετε τη διόρθωση στη δεξιά πλευρά του πίνακα. Σε αυτήν την περίπτωση, στην τιμή $42"$, που βρίσκεται στον πίνακα, πρέπει να προσθέσετε τη διόρθωση για $2"$, που ισούται με $0,0006$. Παίρνουμε:
$\sin17°44"=0,304+0,0006=0,3046$.
Για να βρούμε την τιμή του $\sin17°47"$, χρησιμοποιούμε επίσης τη διόρθωση στη δεξιά πλευρά του πίνακα, μόνο σε αυτήν την περίπτωση λαμβάνουμε ως βάση την τιμή του $\sin17°48"$ και αφαιρούμε τη διόρθωση για $1"$:
$\sin17°47"=0,3057-0,0003=0,3054$.
Κατά τον υπολογισμό των συνημίτονων, εκτελούμε παρόμοιες ενέργειες, αλλά κοιτάμε τις μοίρες στη δεξιά στήλη και τα λεπτά στην κάτω στήλη του πίνακα. Για παράδειγμα, $\cos20°=0,9397$.
Δεν υπάρχουν διορθώσεις για τιμές εφαπτομένης έως $90°$ και μικρής γωνίας συνεφαπτομένης. Για παράδειγμα, ας βρούμε $\tan 78°37"$, που σύμφωνα με τον πίνακα είναι $4.967$.
Ξεκινάμε τη μελέτη μας για την τριγωνομετρία με ένα ορθογώνιο τρίγωνο. Ας ορίσουμε τι είναι το ημίτονο και το συνημίτονο, καθώς και την εφαπτομένη και την συνεφαπτομένη μιας οξείας γωνίας. Αυτά είναι τα βασικά της τριγωνομετρίας.
Θυμηθείτε ότι ορθή γωνίαείναι γωνία ίση με 90 μοίρες. Με άλλα λόγια, η μισή από την ξεδιπλωμένη γωνία.
Κοφτερή γωνία- λιγότερο από 90 μοίρες.
Αμβλεία γωνία- μεγαλύτερη από 90 μοίρες. Σε σχέση με μια τέτοια γωνία, το "αμβλύ" δεν είναι προσβολή, αλλά μαθηματικός όρος :-)
Ας σχεδιάσουμε ένα ορθογώνιο τρίγωνο. Μια ορθή γωνία συνήθως συμβολίζεται . Σημειώστε ότι η πλευρά απέναντι από τη γωνία συμβολίζεται με το ίδιο γράμμα, μόνο μικρό. Έτσι, η πλευρά που βρίσκεται απέναντι από τη γωνία Α συμβολίζεται.
Μια γωνία συμβολίζεται με το αντίστοιχο ελληνικό γράμμα.

ΥποτείνουσαΟρθογώνιο τρίγωνο είναι η πλευρά απέναντι από τη σωστή γωνία.
Πόδια- πλευρές απέναντι από αιχμηρές γωνίες.
Το πόδι απέναντι από τη γωνία ονομάζεται απεναντι απο(σε σχέση με τη γωνία). Το άλλο πόδι, που βρίσκεται στη μία πλευρά της γωνίας, ονομάζεται γειτονικός.
ΚόλποςΗ οξεία γωνία σε ένα ορθογώνιο τρίγωνο είναι ο λόγος του απέναντι σκέλους προς την υποτείνουσα:
Συνημίτονοοξεία γωνία σε ορθογώνιο τρίγωνο - η αναλογία του διπλανού σκέλους προς την υποτείνουσα:
Εφαπτομένοςοξεία γωνία σε ορθογώνιο τρίγωνο - ο λόγος του απέναντι σκέλους προς το παρακείμενο:
Ένας άλλος (ισοδύναμος) ορισμός: η εφαπτομένη μιας οξείας γωνίας είναι ο λόγος του ημιτόνου μιας γωνίας προς το συνημίτονό της:
Συνεφαπτομένηοξεία γωνία σε ορθογώνιο τρίγωνο - η αναλογία του διπλανού σκέλους προς το αντίθετο (ή, ισοδύναμα, η αναλογία συνημιτόνου προς ημίτονο):
Δώστε προσοχή στις βασικές αναλογίες για ημίτονο, συνημίτονο, εφαπτομένη και συνεφαπτομένη, που δίνονται παρακάτω. Θα μας είναι χρήσιμοι στην επίλυση προβλημάτων.

Ας αποδείξουμε μερικά από αυτά.
Εντάξει, δώσαμε ορισμούς και γράψαμε τύπους. Γιατί όμως χρειαζόμαστε ημίτονο, συνημίτονο, εφαπτομένη και συνεφαπτομένη;
Ξέρουμε ότι το άθροισμα των γωνιών οποιουδήποτε τριγώνου είναι.
Γνωρίζουμε τη σχέση μεταξύ κόμματαορθογώνιο τρίγωνο. Αυτό είναι το Πυθαγόρειο θεώρημα: .
Αποδεικνύεται ότι γνωρίζοντας δύο γωνίες σε ένα τρίγωνο, μπορείτε να βρείτε την τρίτη. Γνωρίζοντας δύο πλευρές σε ένα ορθογώνιο τρίγωνο, μπορείτε να βρείτε την τρίτη. Έτσι, για τις γωνίες - την αναλογία τους, για τις πλευρές - τη δική τους. Τι να κάνετε όμως αν σε ένα ορθογώνιο τρίγωνο είναι γνωστές μια γωνία (εκτός από μια ορθή) και μια πλευρά, αλλά πρέπει να βρείτε άλλες πλευρές;

Αυτό αντιμετώπιζαν οι άνθρωποι στο παρελθόν, φτιάχνοντας χάρτες της περιοχής και του έναστρου ουρανού. Εξάλλου, δεν είναι πάντα δυνατό να μετρηθούν απευθείας όλες οι πλευρές ενός τριγώνου.
Ημίτονο, συνημίτονο και εφαπτομένη - ονομάζονται επίσης τριγωνομετρικές συναρτήσεις της γωνίας- δώστε την αναλογία μεταξύ κόμματακαι γωνίεςτρίγωνο. Γνωρίζοντας τη γωνία, μπορείτε να βρείτε όλες τις τριγωνομετρικές της συναρτήσεις χρησιμοποιώντας ειδικούς πίνακες. Και γνωρίζοντας τα ημίτονο, τα συνημίτονα και τις εφαπτομένες των γωνιών ενός τριγώνου και μιας από τις πλευρές του, μπορείτε να βρείτε τα υπόλοιπα.
Θα σχεδιάσουμε επίσης έναν πίνακα τιμών ημιτόνου, συνημίτονος, εφαπτομένης και συνεφαπτομένης για "καλές" γωνίες από έως.
Παρατηρήστε τις δύο κόκκινες παύλες στον πίνακα. Για τις αντίστοιχες τιμές των γωνιών, η εφαπτομένη και η συνεφαπτομένη δεν υπάρχουν.
Ας αναλύσουμε αρκετά προβλήματα στην τριγωνομετρία από τις εργασίες του Bank of FIPI.
1. Σε ένα τρίγωνο, η γωνία είναι , . Εύρημα .
Το πρόβλημα λύνεται σε τέσσερα δευτερόλεπτα.
Επειδή η , .
2. Σε ένα τρίγωνο, η γωνία είναι , , . Εύρημα .

Ας βρούμε με το Πυθαγόρειο θεώρημα.
Το πρόβλημα λύθηκε.
Συχνά σε προβλήματα υπάρχουν τρίγωνα με γωνίες και ή με γωνίες και . Απομνημονεύστε τις βασικές αναλογίες για αυτούς από καρδιάς!

Για ένα τρίγωνο με γωνίες και το σκέλος απέναντι από τη γωνία στο είναι ίσο με το ήμισυ της υποτείνουσας.
Ένα τρίγωνο με γωνίες και είναι ισοσκελές. Σε αυτό, η υποτείνουσα είναι φορές μεγαλύτερη από το πόδι.
Θεωρήσαμε προβλήματα για την επίλυση ορθογωνίων τριγώνων - δηλαδή για την εύρεση άγνωστων πλευρών ή γωνιών. Αλλά δεν είναι μόνο αυτό! Στις παραλλαγές της εξέτασης στα μαθηματικά, υπάρχουν πολλές εργασίες όπου εμφανίζεται το ημίτονο, το συνημίτονο, η εφαπτομένη ή η συνεφαπτομένη της εξωτερικής γωνίας του τριγώνου. Περισσότερα για αυτό στο επόμενο άρθρο.
Στοιχεία αναφοράς για την εφαπτομένη (tg x) και την συνεφαπτομένη (ctg x). Γεωμετρικός ορισμός, ιδιότητες, γραφήματα, τύποι. Πίνακας εφαπτομένων και συνεφαπτομένων, παραγώγων, ολοκληρωμάτων, επεκτάσεων σειρών. Εκφράσεις μέσω μιγαδικών μεταβλητών. Σύνδεση με υπερβολικές συναρτήσεις.
Γεωμετρικός ορισμός

|BD| - το μήκος του τόξου ενός κύκλου με κέντρο το σημείο Α.
α είναι η γωνία που εκφράζεται σε ακτίνια.
Εφαπτομένη ( tgα) είναι μια τριγωνομετρική συνάρτηση που εξαρτάται από τη γωνία α μεταξύ της υποτείνουσας και του σκέλους ενός ορθογωνίου τριγώνου, ίση με τον λόγο του μήκους του απέναντι σκέλους |BC| στο μήκος του διπλανού ποδιού |AB| .
Συμεφαπτομένη ( ctgα) είναι μια τριγωνομετρική συνάρτηση που εξαρτάται από τη γωνία α μεταξύ της υποτείνουσας και του σκέλους ενός ορθογωνίου τριγώνου, ίση με τον λόγο του μήκους του διπλανού σκέλους |AB| στο μήκος του απέναντι σκέλους |π.Χ.| .
Εφαπτομένος
Οπου n- ολόκληρος.
Στη δυτική λογοτεχνία, η εφαπτομένη συμβολίζεται ως εξής:
.
;
;
.
Γράφημα της εφαπτομένης συνάρτησης, y = tg x

Συνεφαπτομένη
Οπου n- ολόκληρος.
Στη δυτική βιβλιογραφία, η συνεφαπτομένη συμβολίζεται ως εξής:
.
Υιοθετήθηκε επίσης ο ακόλουθος συμβολισμός:
;
;
.
Γράφημα της συνεπαπτομένης, y = ctg x

Ιδιότητες εφαπτομένης και συνεφαπτομένης
Περιοδικότης
Συναρτήσεις y= tg xκαι y= ctg xείναι περιοδικές με περίοδο π.
Ισοτιμία
Οι συναρτήσεις εφαπτομένη και συνεφαπτομένη είναι περιττές.
Τομείς ορισμού και αξιών, αύξουσα, φθίνουσα
Οι συναρτήσεις εφαπτομένη και συνεφαπτομένη είναι συνεχείς στο πεδίο ορισμού τους (δείτε την απόδειξη της συνέχειας). Οι κύριες ιδιότητες της εφαπτομένης και της συνεφαπτομένης παρουσιάζονται στον πίνακα ( n- ακέραιος).
| y= tg x | y= ctg x | |
| Πεδίο εφαρμογής και συνέχεια | ||
| Εύρος τιμών | -∞ < y < +∞ | -∞ < y < +∞ |
| Αύξουσα | - | |
| Φθίνων | - | |
| Ακρα | - | - |
| Μηδενικά, y= 0 | ||
| Σημεία τομής με τον άξονα y, x = 0 | y= 0 | - |
ΜΑΘΗΜΑΤΙΚΟΙ τυποι
Εκφράσεις ως προς το ημίτονο και το συνημίτονο
;
;
;
;
;
Τύποι για την εφαπτομένη και την συνεφαπτομένη του αθροίσματος και της διαφοράς
Οι υπόλοιποι τύποι είναι εύκολο να ληφθούν, για παράδειγμα
Προϊόν των εφαπτομένων
Ο τύπος για το άθροισμα και τη διαφορά των εφαπτομένων
Αυτός ο πίνακας δείχνει τις τιμές των εφαπτομένων και των συνεφαπτομένων για ορισμένες τιμές του ορίσματος. 
Εκφράσεις ως προς τους μιγαδικούς αριθμούς
Εκφράσεις ως προς τις υπερβολικές συναρτήσεις
;
;
Παράγωγα
; .
.
Παράγωγος της νης τάξης ως προς τη μεταβλητή x της συνάρτησης :
.
Παραγωγή τύπων για εφαπτομένη > > > ; για συνεφαπτομένη > > >
Ολοκληρώματα
Επεκτάσεις σε σειρές
Για να λάβετε την επέκταση της εφαπτομένης σε δυνάμεις του x, πρέπει να λάβετε αρκετούς όρους της επέκτασης σε μια σειρά ισχύος για τις συναρτήσεις αμαρτία xκαι cos xκαι διαιρέστε αυτά τα πολυώνυμα το ένα στο άλλο, . αυτο εχει ως αποτελεσμα τους παρακάτω τύπους.
Στο .
στο .
όπου B n- Αριθμοί Μπερνούλι. Καθορίζονται είτε από τη σχέση υποτροπής:
;
;
όπου .
Ή σύμφωνα με τον τύπο Laplace: 
Αντίστροφες συναρτήσεις
Οι αντίστροφες συναρτήσεις της εφαπτομένης και της συνεφαπτομένης είναι τοξοεφαπτομένη και τοξοεφαπτομένη, αντίστοιχα.
Arctangent, arctg
, όπου n- ολόκληρος.
Εφαπτομένη τόξου, arcctg
, όπου n- ολόκληρος.
Βιβλιογραφικές αναφορές:
ΣΕ. Bronstein, Κ.Α. Semendyaev, Εγχειρίδιο Μαθηματικών για Μηχανικούς και Φοιτητές Ανώτατων Εκπαιδευτικών Ιδρυμάτων, Lan, 2009.
G. Korn, Εγχειρίδιο Μαθηματικών για Ερευνητές και Μηχανικούς, 2012.
1. Τριγωνομετρικές συναρτήσειςείναι στοιχειώδεις συναρτήσεις των οποίων το όρισμα είναι γωνία. Οι τριγωνομετρικές συναρτήσεις περιγράφουν τη σχέση μεταξύ πλευρών και οξειών γωνιών σε ένα ορθογώνιο τρίγωνο. Οι τομείς εφαρμογής των τριγωνομετρικών συναρτήσεων είναι εξαιρετικά διαφορετικοί. Έτσι, για παράδειγμα, οποιεσδήποτε περιοδικές διεργασίες μπορούν να αναπαρασταθούν ως άθροισμα τριγωνομετρικών συναρτήσεων (σειρά Fourier). Αυτές οι συναρτήσεις εμφανίζονται συχνά κατά την επίλυση διαφορικών και συναρτησιακών εξισώσεων.
2. Οι τριγωνομετρικές συναρτήσεις περιλαμβάνουν τις ακόλουθες 6 συναρτήσεις: κόλπος, συνημίτονο, εφαπτομένος,συνεφαπτομένη, διατέμνωνκαι συντεμνούσα. Για καθεμία από αυτές τις συναρτήσεις, υπάρχει μια αντίστροφη τριγωνομετρική συνάρτηση.
3. Είναι βολικό να εισάγουμε τον γεωμετρικό ορισμό των τριγωνομετρικών συναρτήσεων χρησιμοποιώντας κύκλος μονάδας. Το παρακάτω σχήμα δείχνει έναν κύκλο με ακτίνα r=1. Το σημείο M(x,y) σημειώνεται στον κύκλο. Η γωνία μεταξύ του διανύσματος ακτίνας OM και της θετικής κατεύθυνσης του άξονα Ox είναι α.
4. κόλποςη γωνία α είναι ο λόγος της τεταγμένης y του σημείου M(x,y) προς την ακτίνα r:
sinα=y/r.
Αφού r=1, τότε το ημίτονο ισούται με την τεταγμένη του σημείου M(x,y).
5. συνημίτονοη γωνία α είναι ο λόγος της τετμημένης x του σημείου M(x,y) προς την ακτίνα r:
cosα=x/r
6. εφαπτομένοςη γωνία α είναι ο λόγος της τεταγμένης y του σημείου M(x,y) προς την τετμημένη του x:
tana=y/x,x≠0
7. Συνεφαπτομένηη γωνία α είναι ο λόγος της τετμημένης x του σημείου M(x,y) προς την τεταγμένη του y:
cotα=x/y,y≠0
8. ΔιατέμνωνΗ γωνία α είναι ο λόγος της ακτίνας r προς την τετμημένη x του σημείου M(x,y):
secα=r/x=1/x,x≠0
9. ΣυντεμνούσαΗ γωνία α είναι ο λόγος της ακτίνας r προς την τεταγμένη y του σημείου M(x,y):
cscα=r/y=1/y,y≠0
10. Στον μοναδιαίο κύκλο, οι προβολές x, y των σημείων M(x,y) και η ακτίνα r σχηματίζουν ορθογώνιο τρίγωνο, στο που x,yείναι τα πόδια και το r είναι η υποτείνουσα. Επομένως, οι παραπάνω ορισμοί των τριγωνομετρικών συναρτήσεων όπως εφαρμόζονται σε ένα ορθογώνιο τρίγωνο διατυπώνονται ως εξής:
κόλποςΗ γωνία α είναι ο λόγος του αντίθετου σκέλους προς την υποτείνουσα.
συνημίτονοΗ γωνία α είναι ο λόγος του διπλανού σκέλους προς την υποτείνουσα.
εφαπτομένοςγωνία α ονομάζεται το αντίθετο σκέλος από το διπλανό.
Συνεφαπτομένηγωνία α ονομάζεται το διπλανό σκέλος στο αντίθετο.
ΔιατέμνωνΗ γωνία α είναι ο λόγος της υποτείνουσας προς το διπλανό σκέλος.
ΣυντεμνούσαΗ γωνία α είναι ο λόγος της υποτείνουσας προς το αντίθετο σκέλος.
11. γράφημα ημιτονικής συνάρτησης
y=sinx, τομέας: x∈R, τομέας: −1≤sinx≤1
12. Γράφημα της συνημίτονος
y=cosx, τομέας: x∈R, εύρος: −1≤cosx≤1
13. γράφημα συνάρτησης εφαπτομένης 14. Γράφημα της συνεπαπτομένης 15. Γράφημα της συνάρτησης τομής
y=tanx, τομέας: x∈R,x≠(2k+1)π/2, τομέας: −∞ 
y=cotx, τομέας: x∈R,x≠kπ, τομέας: −∞ 
y=secx, τομέας: x∈R,x≠(2k+1)π/2, τομέας: secx∈(−∞,−1]∪∪)
Η επιλογή των συντακτών


