Tabelul funcțiilor trigonometrice. Funcții trigonometrice

Să presupunem că Ahile aleargă de zece ori mai repede decât țestoasa și este la o mie de pași în spatele ei. În timpul în care Ahile parcurge această distanță, țestoasa se târăște o sută de pași în aceeași direcție. Când Ahile a alergat o sută de pași, țestoasa se va târa încă zece pași și așa mai departe. Procesul va continua la nesfârșit, Ahile nu va ajunge niciodată din urmă cu broasca țestoasă.

Acest raționament a devenit un șoc logic pentru toate generațiile următoare. Aristotel, Diogene, Kant, Hegel, Gilbert... Toți, într-un fel sau altul, au considerat aporii lui Zenon. Șocul a fost atât de puternic încât " ... discuțiile continuă în prezent, comunitatea științifică nu a reușit încă să ajungă la o opinie comună despre esența paradoxurilor... analiza matematică, teoria mulțimilor, noi abordări fizice și filozofice au fost implicate în studiul problemei ; niciunul dintre ele nu a devenit o soluție universal acceptată la problemă...„[Wikipedia,” Aporii lui Zeno „]. Toată lumea înțelege că sunt păcăliți, dar nimeni nu înțelege ce este înșelăciunea.

Din punctul de vedere al matematicii, Zenon în aporia sa a demonstrat clar trecerea de la valoare la. Această tranziție implică aplicarea în loc de constante. Din câte am înțeles, aparatul matematic pentru aplicarea unităților de măsură variabile fie nu a fost încă dezvoltat, fie nu a fost aplicat aporiei lui Zenon. Aplicarea logicii noastre obișnuite ne duce într-o capcană. Noi, prin inerția gândirii, aplicăm reciprocului unități constante de timp. Din punct de vedere fizic, aceasta pare o încetinire a timpului până când se oprește complet în momentul în care Ahile ajunge din urmă cu țestoasa. Dacă timpul se oprește, Ahile nu mai poate depăși țestoasa.

Dacă întoarcem logica cu care suntem obișnuiți, totul cade la locul său. Ahile aleargă cu o viteză constantă. Fiecare segment ulterior al traseului său este de zece ori mai scurt decât cel anterior. În consecință, timpul petrecut pentru depășirea acestuia este de zece ori mai mic decât cel anterior. Dacă aplicăm conceptul de „infinit” în această situație, atunci ar fi corect să spunem „Achile va depăși infinit rapid broasca țestoasă”.

Cum să eviți această capcană logică? Rămâneți în unități constante de timp și nu treceți la valori reciproce. În limba lui Zeno, arată astfel:

În timpul necesar lui Ahile să alerge o mie de pași, țestoasa se târăște o sută de pași în aceeași direcție. În următorul interval de timp, egal cu primul, Ahile va alerga încă o mie de pași, iar țestoasa se va târa o sută de pași. Acum Ahile este cu opt sute de pași înaintea țestoasei.

Această abordare descrie în mod adecvat realitatea fără niciun paradox logic. Dar nu este solutie completa Probleme. Afirmația lui Einstein despre insurmontabilitatea vitezei luminii este foarte asemănătoare cu aporia lui Zeno „Achile și broasca țestoasă”. Încă trebuie să studiem, să regândim și să rezolvăm această problemă. Iar soluția trebuie căutată nu în număr infinit de mare, ci în unități de măsură.

O altă aporie interesantă a lui Zeno spune despre o săgeată zburătoare:

O săgeată zburătoare este nemișcată, deoarece în fiecare moment de timp este în repaus și, deoarece este în repaus în fiecare moment de timp, este întotdeauna în repaus.

În această aporie, paradoxul logic este depășit foarte simplu - este suficient să clarificăm că în fiecare moment de timp săgeata zburătoare este în repaus în diferite puncte din spațiu, ceea ce, de fapt, este mișcare. Mai este un punct de remarcat aici. Dintr-o fotografie a unei mașini pe șosea, este imposibil să se determine nici faptul mișcării acesteia, nici distanța până la ea. Pentru a determina fapta mișcării mașinii, sunt necesare două fotografii realizate din același punct în momente diferite în timp, dar nu pot fi folosite pentru a determina distanța. Pentru a determina distanța până la mașină, aveți nevoie de două fotografii făcute puncte diferite spațiu la un moment dat, dar este imposibil să determinați faptul deplasării din ele (în mod firesc, sunt încă necesare date suplimentare pentru calcule, trigonometria vă va ajuta). Ceea ce vreau să subliniez în special este că două puncte în timp și două puncte în spațiu sunt două lucruri diferite care nu trebuie confundate, deoarece oferă oportunități diferite de explorare.

miercuri, 4 iulie 2018

Foarte bine diferențele dintre set și multiset sunt descrise în Wikipedia. Ne uitam.

După cum puteți vedea, „multimea nu poate avea două elemente identice”, dar dacă există elemente identice în set, un astfel de set se numește „multiset”. Ființele rezonabile nu vor înțelege niciodată o asemenea logică a absurdității. Acesta este nivelul papagalilor vorbitori și al maimuțelor dresate, în care mintea este absentă din cuvântul „complet”. Matematicienii acționează ca formatori obișnuiți, propovăduindu-ne ideile lor absurde.

Pe vremuri, inginerii care au construit podul se aflau într-o barcă sub pod în timpul testelor podului. Dacă podul s-a prăbușit, inginerul mediocru a murit sub dărâmăturile creației sale. Dacă podul putea rezista la sarcină, talentatul inginer a construit alte poduri.

Indiferent de cât de matematicieni se ascund în spatele expresiei „mind-mă, sunt în casă”, sau mai degrabă „matematica studiază concepte abstracte”, există un singur cordon ombilical care le leagă indisolubil de realitatea. Acest cordon ombilical este bani. Să aplicăm teoria mulțimilor matematicienilor înșiși.

Am studiat foarte bine matematica și acum stăm la casierie, plătim salarii. Aici vine un matematician la noi pentru banii lui. Numărăm întreaga sumă pentru el și o întindem pe masa noastră în grămezi diferite, în care punem bancnote de aceeași valoare. Apoi luăm câte o bancnotă din fiecare grămadă și îi dăm matematicianului „setul său de salariu matematic”. Explicăm la matematică că va primi restul bancnotelor doar atunci când va dovedi că mulțimea fără elemente identice nu este egală cu mulțimea cu elemente identice. Aici începe distracția.

În primul rând, logica deputaților va funcționa: „puteți aplica și altora, dar mie nu!” În plus, vor începe asigurările că există numere diferite de bancnote pe bancnotele de aceeași valoare nominală, ceea ce înseamnă că acestea nu pot fi considerate elemente identice. Ei bine, numărăm salariul în monede - nu există numere pe monede. Aici, matematicianul își va aminti frenetic de fizică: diferite monede au cantități diferite de murdărie, structură cristalină iar aranjamentul atomilor din fiecare monedă este unic...

Și acum am cel mai mult interes Întreabă: unde este granița dincolo de care elementele unui multiset se transformă în elemente ale unei mulțimi și invers? O astfel de linie nu există - totul este decis de șamani, știința aici nu este nici măcar aproape.

Uite aici. Selectăm stadioane de fotbal cu aceeași suprafață de teren. Aria câmpurilor este aceeași, ceea ce înseamnă că avem un multiset. Dar dacă luăm în considerare numele acelorași stadioane, obținem multe, pentru că numele sunt diferite. După cum puteți vedea, același set de elemente este atât un set cât și un multiset în același timp. Cât de corect? Și aici matematicianul-șaman-shuller scoate un as de atu din mânecă și începe să ne vorbească fie despre un set, fie despre un multiset. În orice caz, ne va convinge că are dreptate.

Pentru a înțelege cum funcționează șamanii moderni cu teoria mulțimilor, legând-o de realitate, este suficient să răspundem la o întrebare: prin ce diferă elementele unui set de elementele altui set? Vă voi arăta, fără niciun „conceput ca nu un singur întreg” sau „neconceput ca un singur întreg”.

Duminică, 18 martie 2018

Suma cifrelor unui număr este un dans al șamanilor cu o tamburină, care nu are nimic de-a face cu matematica. Da, la lecțiile de matematică suntem învățați să găsim suma cifrelor unui număr și să o folosim, dar ei sunt șamani pentru asta, pentru a-și învăța descendenții abilitățile și înțelepciunea, altfel șamanii pur și simplu vor muri.

Ai nevoie de dovezi? Deschideți Wikipedia și încercați să găsiți pagina „Suma cifrelor unui număr”. Ea nu există. Nu există o formulă în matematică prin care să poți găsi suma cifrelor oricărui număr. La urma urmei, numerele sunt simboluri grafice cu care scriem numere, iar în limbajul matematicii, sarcina sună astfel: „Găsiți suma simbolurilor grafice care reprezintă orice număr”. Matematicienii nu pot rezolva această problemă, dar șamanii o pot face în mod elementar.

Să ne dăm seama ce și cum facem pentru a găsi suma cifrelor unui număr dat. Și așa, să presupunem că avem numărul 12345. Ce trebuie făcut pentru a găsi suma cifrelor acestui număr? Să luăm în considerare toți pașii în ordine.

1. Notează numărul pe o foaie de hârtie. Ce am făcut? Am convertit numărul într-un simbol grafic numeric. Aceasta nu este o operație matematică.

2. Am tăiat o imagine primită în mai multe imagini care conțin numere separate. Decuparea unei imagini nu este o operație matematică.

3. Convertiți caracterele grafice individuale în numere. Aceasta nu este o operație matematică.

4. Adunați numerele rezultate. Acum asta e matematica.

Suma cifrelor numărului 12345 este 15. Acestea sunt „cursurile de tăiere și cusut” de la șamani folosite de matematicieni. Dar asta nu este tot.

Din punct de vedere al matematicii, nu contează în ce sistem de numere scriem numărul. Deci, în sisteme diferite luând în calcul, suma cifrelor aceluiași număr va fi diferită. În matematică, sistemul numeric este indicat ca indice în dreapta numărului. Cu un număr mare 12345, nu vreau să-mi păcălesc capul, luați în considerare numărul 26 din articolul despre. Să scriem acest număr în sisteme de numere binar, octal, zecimal și hexazecimal. Nu vom lua în considerare fiecare pas la microscop, am făcut-o deja. Să ne uităm la rezultat.

După cum puteți vedea, în sisteme numerice diferite, suma cifrelor aceluiași număr este diferită. Acest rezultat nu are nimic de-a face cu matematica. Este ca și cum găsirea ariei unui dreptunghi în metri și centimetri ți-ar da rezultate complet diferite.

Zero în toate sistemele de numere arată la fel și nu are sumă de cifre. Acesta este un alt argument în favoarea faptului că . O întrebare pentru matematicieni: cum se notează în matematică ceea ce nu este un număr? Ce, pentru matematicieni, nu există decât numere? Pentru șamani, pot permite acest lucru, dar pentru oameni de știință, nu. Realitatea nu este doar despre cifre.

Rezultatul obținut ar trebui considerat ca o dovadă că sistemele numerice sunt unități de măsură ale numerelor. La urma urmei, nu putem compara numerele cu unități de măsură diferite. Dacă aceleași acțiuni cu diferite unități de măsură ale aceleiași mărimi duc la rezultate diferite după compararea lor, atunci acest lucru nu are nimic de-a face cu matematica.

Ce este matematica reală? Acesta este momentul în care rezultatul unei acțiuni matematice nu depinde de valoarea numărului, de unitatea de măsură folosită și de cine efectuează această acțiune.

Ai! Asta nu este toaleta femeilor?
- Femeie tânără! Acesta este un laborator pentru studierea sfințeniei nedefinite a sufletelor la înălțarea la cer! Nimbus în partea de sus și săgeată în sus. Ce altă toaletă?

Femeie... Un halou deasupra și o săgeată în jos sunt masculin.

Dacă aveți o astfel de operă de artă de design fulgerând în fața ochilor dvs. de mai multe ori pe zi,

Atunci nu este surprinzător că găsiți brusc o pictogramă ciudată în mașina dvs.:

Personal, fac un efort pe mine să văd minus patru grade la o persoană care face caca (o poză) (compunere din mai multe imagini: semnul minus, numărul patru, desemnarea grade). Și nu o consider pe fata asta o proastă care nu știe fizică. Ea are doar un arc stereotip al percepției imaginilor grafice. Și matematicienii ne învață asta tot timpul. Iată un exemplu.

1A nu este „minus patru grade” sau „unu a”. Acesta este „omul care face caca” sau numărul „douăzeci și șase” în sistemul numeric hexazecimal. Acei oameni care lucrează constant în acest sistem numeric percep automat numărul și litera ca un simbol grafic.

În articol, vom înțelege pe deplin cum arată tabel de valori trigonometrice, sinus, cosinus, tangentă și cotangentă. Se consideră valoarea de bază a funcțiilor trigonometrice, dintr-un unghi de 0,30,45,60,90,...,360 de grade. Și să vedem cum să folosim aceste tabele în calcularea valorii funcțiilor trigonometrice.
Mai întâi luați în considerare tabelul cosinus, sinus, tangente și cotangente dintr-un unghi de 0, 30, 45, 60, 90,.. grade. Definirea acestor mărimi face posibilă determinarea valorii funcțiilor unghiurilor de 0 și 90 de grade:

sin 0 0 \u003d 0, cos 0 0 \u003d 1. tg 00 \u003d 0, cotangenta lui 00 va fi nedefinită
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, tangenta lui 90 0 va fi nedefinită

Dacă luăm triunghiuri dreptunghiulare ale căror unghiuri sunt de la 30 la 90 de grade. Primim:

sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, ctg 60 0 = √3/3

Reprezentăm toate valorile obținute în formular tabel trigonometric:

Tabel de sinusuri, cosinus, tangente și cotangente!

Dacă folosim formula de turnare, tabelul nostru va crește, se vor adăuga valori pentru unghiuri de până la 360 de grade. Va arata ca:

De asemenea, pe baza proprietăților periodicității, tabelul poate fi mărit dacă înlocuim unghiurile cu 0 0 +360 0 *z .... 330 0 +360 0 *z, în care z este un număr întreg. În acest tabel, este posibil să se calculeze valoarea tuturor unghiurilor corespunzătoare punctelor dintr-un singur cerc.

Să vedem clar cum să folosim tabelul în soluție.
Totul este foarte simplu. Deoarece valoarea de care avem nevoie se află în punctul de intersecție al celulelor de care avem nevoie. De exemplu, să luăm cos unui unghi de 60 de grade, în tabel va arăta astfel:

În tabelul final al principalelor valori ale funcțiilor trigonometrice, acționăm în același mod. Dar în acest tabel este posibil să aflăm cât de mult va fi tangenta dintr-un unghi de 1020 de grade, ea = -√3 Să verificăm 1020 0 = 300 0 +360 0 *2. Să găsim masa.

masa Bradis. Pentru sinus, cosinus, tangentă și cotangentă.

Tabelele lui Bradys sunt împărțite în mai multe părți, ele constau din tabele de cosinus și sinus, tangentă și cotangentă - care este împărțită în două părți (tg de un unghi de până la 90 de grade și ctg de unghiuri mici).

Sinus și cosinus

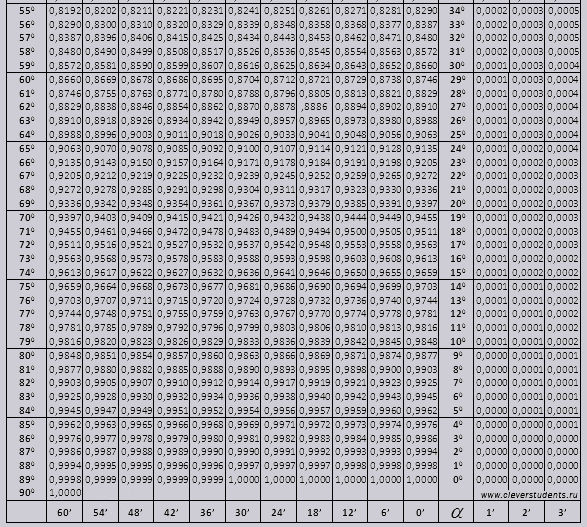
unghi tg de la 00 la 760, unghi ctg de la 140 la 900.

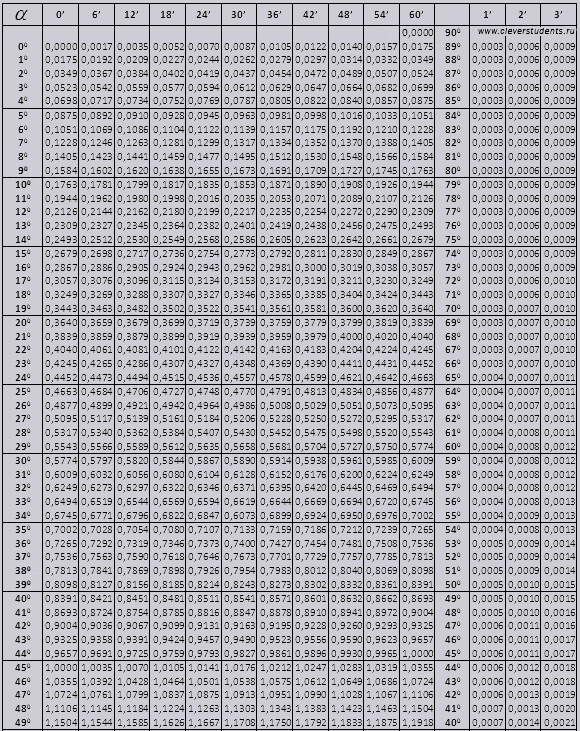
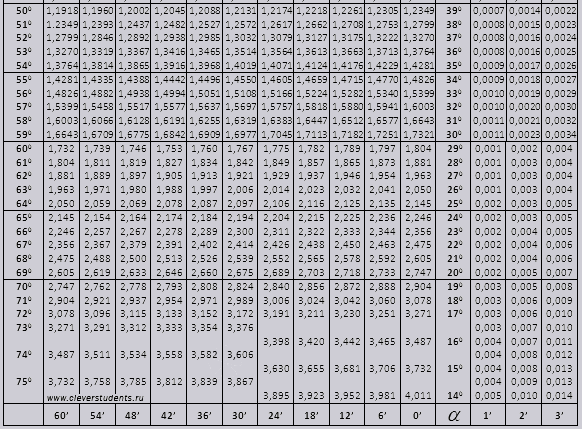
tg până la 900 și ctg unghiuri mici.

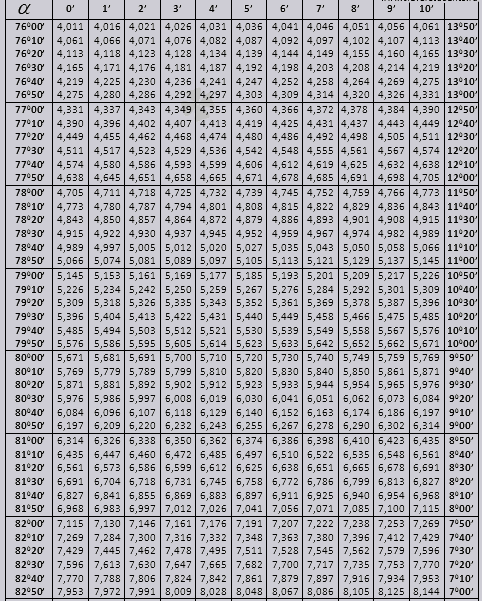
Să ne dăm seama cum să folosim tabelele Bradis în rezolvarea problemelor.

Să găsim denumirea sin (desemnarea în coloana de la marginea din stânga) 42 de minute (denumirea este pe linia de sus). Prin trecere căutăm o desemnare, aceasta este = 0,3040.

Valorile minutelor sunt indicate cu un interval de șase minute, dacă valoarea de care avem nevoie se încadrează în acest interval. Să luăm 44 de minute și în tabel sunt doar 42. Luăm 42 ca bază și folosim coloane suplimentare în partea dreapta, luăm al 2-lea amendament și adăugăm la 0,3040 + 0,0006 obținem 0,3046.

Cu sin 47 min, luăm 48 min ca bază și scădem 1 corecție din ea, adică 0,3057 - 0,0003 = 0,3054

Când calculăm cos, lucrăm similar cu sin, doar că luăm ca bază rândul de jos al tabelului. De exemplu cos 20 0 = 0,9397

Valorile tg ale unui unghi de până la 90 0 și cot ale unui unghi mic sunt corecte și nu există corecții în ele. De exemplu, găsiți tg 78 0 37min = 4,967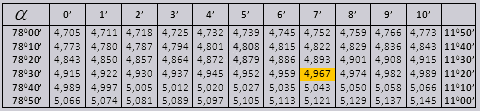


și ctg 20 0 13 min = 25,83

Ei bine, am acoperit principalul tabele trigonometrice. Sperăm că aceste informații v-au fost extrem de utile. Întrebările tale de pe mese, dacă există, asigurați-vă că scrieți în comentarii!

Notă: Apărătoare de perete - o placă de protecție pentru protejarea pereților. Urmați link-ul pentru aripi fără perete și fără cadru (http://www.spi-polymer.ru/otboyniki/) și aflați mai multe.

TABEL DE VALORI ALE FUNCŢIILOR TRIGONOMETRICE

Tabelul de valori ale funcțiilor trigonometrice este întocmit pentru unghiuri de 0, 30, 45, 60, 90, 180, 270 și 360 de grade și unghiurile corespunzătoare acestora în radiani. Dintre funcțiile trigonometrice, tabelul arată sinusul, cosinusul, tangenta, cotangenta, secanta și cosecanta. Pentru comoditatea rezolvării exemplelor școlare, valorile funcțiilor trigonometrice din tabel sunt scrise ca o fracție cu păstrarea semnelor de extragere a rădăcinii pătrate din numere, ceea ce ajută foarte adesea la reducerea expresiilor matematice complexe. Pentru tangentă și cotangentă, valorile unor unghiuri nu pot fi determinate. Pentru valorile tangentei și cotangentei unor astfel de unghiuri, există o liniuță în tabelul de valori ale funcțiilor trigonometrice. Este în general acceptat că tangenta și cotangenta unor astfel de unghiuri este egală cu infinitul. Pe o pagină separată sunt formule pentru reducerea funcțiilor trigonometrice.

Tabelul de valori pentru funcția trigonometrică sinus arată valorile pentru următoarele unghiuri: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 în grad de măsură , care corespunde cu sin 0 pi, sin pi / 6 , sin pi / 4, sin pi / 3, sin pi / 2, sin pi, sin 3 pi / 2, sin 2 pi în măsura radianilor unghiurilor. Masa școlară de sinusuri.

Pentru funcția cosinus trigonometrică, tabelul prezintă valorile pentru următoarele unghiuri: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 în măsură de grade, care corespunde cu cos 0 pi, cos pi la 6, cos pi cu 4, cos pi cu 3, cos pi cu 2, cos pi, cos 3 pi cu 2, cos 2 pi în măsurarea radianilor unghiurilor. Masa școlară de cosinus.

Tabelul trigonometric pentru tangenta funcției trigonometrice oferă valori pentru următoarele unghiuri: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 în măsura în grade, care corespunde cu tg 0 pi, tg pi / 6, tg pi / 4, tg pi/3, tg pi, tg 2 pi în măsurarea radianilor unghiurilor. Următoarele valori ale funcțiilor trigonometrice ale tangentei nu sunt definite tg 90, tg 270, tg pi/2, tg 3 pi/2 și sunt considerate egale cu infinitul.

Pentru funcția trigonometrică cotangentă din tabelul trigonometric, sunt date următoarele unghiuri: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 în grade, care corespunde cu ctg pi / 6, ctg pi / 4, ctg pi / 3 , tg pi / 2, tg 3 pi/2 în măsura radianilor unghiurilor. Următoarele valori ale funcțiilor trigonometrice cotangente nu sunt definite ctg 0, ctg 180, ctg 360, ctg 0 pi, ctg pi, ctg 2 pi și sunt considerate egale cu infinitul.

Valorile funcțiilor trigonometrice secant și cosecant sunt date pentru aceleași unghiuri în grade și radiani ca sinus, cosinus, tangentă, cotangentă.

Tabelul de valori ale funcțiilor trigonometrice ale unghiurilor nestandard arată valorile sinusului, cosinusului, tangentei și cotangentei pentru unghiurile în grade 15, 18, 22,5, 36, 54, 67,5 72 grade și în radiani pi/12 , pi/10, pi/8, pi/5, 3pi/8, 2pi/5 radiani. Valorile funcțiilor trigonometrice sunt exprimate în termeni de fracții și rădăcini pătrate pentru a simplifica reducerea fracțiilor în exemplele școlare.

Încă trei monștri ai trigonometriei. Prima este tangenta de 1,5 grade și jumătate, sau pi împărțit la 120. Al doilea este cosinusul lui pi împărțit la 240, pi/240. Cel mai lung este cosinusul lui pi împărțit la 17, pi/17.

Cercul trigonometric al valorilor funcțiilor sinus și cosinus reprezintă vizual semnele sinusului și cosinusului în funcție de mărimea unghiului. În special pentru blonde, valorile cosinusului sunt subliniate cu o liniuță verde pentru a fi mai puțin confuze. Conversia gradelor în radiani este, de asemenea, foarte clar prezentată, atunci când radianii sunt exprimați prin pi.

Acest tabel trigonometric prezintă valorile sinusului, cosinusului, tangentei și cotangentei pentru unghiuri de la 0 zero la 90 nouăzeci de grade în intervale de un grad. Pentru primele patruzeci și cinci de grade, numele funcțiilor trigonometrice trebuie privite în partea de sus a tabelului. Prima coloană conține grade, valorile sinusurilor, cosinusului, tangentelor și cotangentelor sunt scrise în următoarele patru coloane.

Pentru unghiuri de la patruzeci și cinci de grade până la nouăzeci de grade, numele funcțiilor trigonometrice sunt scrise în partea de jos a tabelului. Ultima coloană conține grade, valorile cosinusului, sinusurilor, cotangentelor și tangentelor sunt scrise în cele patru coloane anterioare. Ar trebui să fiți atenți, deoarece numele funcțiilor trigonometrice din partea inferioară a tabelului trigonometric sunt diferite de numele din partea superioară a tabelului. Sinusurile și cosinusurile sunt interschimbate, la fel ca tangenta și cotangenta. Acest lucru se datorează simetriei valorilor funcțiilor trigonometrice.

Semnele funcțiilor trigonometrice sunt prezentate în figura de mai sus. Sinusul are valori pozitive de la 0 la 180 de grade sau de la 0 la pi. Valorile negative ale sinusului sunt de la 180 la 360 de grade sau de la pi la 2 pi. Valorile cosinusului sunt pozitive de la 0 la 90 și de la 270 la 360 de grade sau de la 0 la 1/2 pi și 3/2 la 2 pi. Tangenta și cotangenta au valori pozitive de la 0 la 90 de grade și de la 180 la 270 de grade, corespunzătoare valorilor de la 0 la 1/2 pi și de la pi la 3/2 pi. Tangenta și cotangenta negativă sunt de la 90 la 180 de grade și de la 270 la 360 de grade sau 1/2 pi la pi și 3/2 pi la 2 pi. Când se determină semnele funcțiilor trigonometrice pentru unghiuri mai mari de 360 ​​de grade sau 2 pi, trebuie utilizate proprietățile de periodicitate ale acestor funcții.

Funcții trigonometrice sinus, tangentă și cotangentă sunt funcții impare. Valorile acestor funcții pentru unghiurile negative vor fi negative. Cosinusul este o funcție trigonometrică uniformă - valoarea cosinusului pentru un unghi negativ va fi pozitivă. Când înmulțiți și împărțiți funcții trigonometrice, trebuie să respectați regulile semnelor.

1. Tabelul de valori pentru funcția trigonometrică sinus arată valorile pentru următoarele unghiuri

   Document

   O pagină separată conține formule de turnare trigonometricfuncții. LA masavalorilepentrutrigonometricfuncțiisinusuluidatvalorilepentruUrmătorulcolțuri: sin 0, sin 30, sin 45 ...

2. Aparatul matematic propus este un analog complet al calculului complex pentru numere hipercomplex n-dimensionale cu orice număr de grade de libertate n și este destinat modelării matematice a neliniarelor.

   Document

   ... funcții egală funcții Imagini. Din această teoremă ar trebui să, ce pentru afland coordonatele U, V, este suficient sa se calculeze funcţie... geometrie; polinar funcții(analogi multidimensionali ai bidimensionali trigonometricfuncții), proprietățile lor, Meseși aplicare; ...

3. Atenţie!
   Există suplimentare
   material în secțiunea specială 555.
   Pentru cei care puternic „nu foarte...”
   Și pentru cei care „foarte mult...”)

   În primul rând, permiteți-mi să vă reamintesc o concluzie simplă, dar foarte utilă din lecția „Ce sunt sinus și cosinus? Ce sunt tangente și cotangente?”

   Iată acea ieșire:

   Sinusul, cosinusul, tangenta și cotangenta sunt strâns legate de unghiurile lor. Știm un lucru, așa că știm altceva.

   Cu alte cuvinte, fiecare unghi are propriul sinus și cosinus fix. Și aproape fiecare are propria tangentă și cotangentă. De ce aproape? Mai multe despre asta mai jos.

   Aceste cunoștințe te vor ajuta foarte mult! Există multe sarcini în care trebuie să treceți de la sinusuri la unghiuri și invers. Pentru asta există masa sinusurilor.În mod similar, pentru locurile de muncă cu cosinus - masa cosinus.Și, ați ghicit, există tabel tangenteși masa cotangente.)

   Tabelele sunt diferite. Cele lungi, unde puteți vedea cu ce, să zicem, sin37 ° 6 'este egal. Deschidem tabelele Bradis, căutăm un unghi de treizeci și șapte de grade șase minute și vedem valoarea de 0,6032. Desigur, amintirea acestui număr (și a miilor de alte valori tabelare) nu este absolut necesară.

   De fapt, în timpul nostru, tabele lungi de cosinus, sinusuri, tangente și cotangente nu sunt cu adevărat necesare. Un calculator bun le înlocuiește complet. Dar nu strică să știi despre existența unor astfel de tabele. Pentru erudiția generală.)

   Atunci de ce această lecție? - tu intrebi.

   Dar de ce. Printre numărul infinit de unghiuri există special, despre care ar trebui să știți toate. Toată geometria școlară și trigonometria sunt construite pe aceste unghiuri. Acesta este un fel de „tabel de înmulțire” al trigonometriei. Dacă nu știi cu ce este sin50°, de exemplu, nimeni nu te va judeca.) Dar dacă nu știi cu ce este sin30°, pregătește-te să obții un binemeritat deuce...

   Astfel de special colțurile sunt, de asemenea, tastate decent. Manualele școlare sunt de obicei oferite cu amabilitate pentru memorare. masa sinusurilor si masa cosinusului pentru șaptesprezece colțuri. Și, desigur, tabel tangente și tabel cotangente pentru aceleaşi şaptesprezece colţuri... Adică. se propune amintirea a 68 de valori. Care, apropo, sunt foarte asemănătoare între ele, se repetă și își schimbă semnele din când în când. Pentru un bărbat fără ideal memorie vizuală- altă problema...)

   Vom merge pe altă cale. Să înlocuim memorarea mecanică cu logica și ingeniozitatea. Apoi trebuie să memorăm 3 (trei!) valori pentru tabelul sinusurilor și tabelul cosinusurilor. Și 3 (trei!) valori pentru tabelul tangentelor și tabelul cotangentelor. Si asta e. Șase valori sunt mai ușor de reținut decât 68, cred...)

   Vom obține toate celelalte valori necesare de la aceste șase folosind o fișă legală puternică. - cerc trigonometric. Dacă nu ai studiat acest subiect, mergi pe link, nu fi leneș. Acest cerc nu este doar pentru această lecție. El este de neînlocuit pentru toată trigonometria deodată. A nu folosi un astfel de instrument este pur și simplu un păcat! Tu nu vrei? E treaba ta. memora masa sinusurilor. masa cosinus. Tabelul tangentei. Masa cotangente. Toate cele 68 de valori pentru diferite unghiuri.)

   Deci, să începem. Pentru început, să împărțim toate aceste unghiuri speciale în trei grupuri.

   Primul grup de colțuri.

   Luați în considerare primul grup colţuri de şaptesprezece special. Acestea sunt 5 unghiuri: 0°, 90°, 180°, 270°, 360°.

   Iată cum arată tabelul de sinusuri, cosinus, tangente și cotangente pentru aceste unghiuri:

   Unghiul x (în grade)	0	90	180	270	360
   Unghiul x (în radiani)	0
   sin x	0	1	0	-1	0
   cos x	1	0	-1	0	1
   tg x	0	nu substantiv	0	nu substantiv	0
   ctg x	nu substantiv	0	nu substantiv	0	nu substantiv

   Cei care vor să-și amintească - amintiți-vă. Dar trebuie să spun imediat că toate acestea și zerourile sunt foarte confuze în capul meu. Mult mai puternic decât doriți.) Prin urmare, activăm logica și cercul trigonometric.

   Desenăm un cerc și marchem aceleași unghiuri pe el: 0°, 90°, 180°, 270°, 360°. Am marcat aceste colțuri cu puncte roșii:

   

   Puteți vedea imediat care este particularitatea acestor colțuri. Da! Acestea sunt colțurile care cad exact pe axa de coordonate! De fapt, de aceea oamenii se încurcă... Dar noi nu ne vom încurca. Să ne dăm seama cum să găsim funcțiile trigonometrice ale acestor unghiuri fără prea multă memorare.

   Apropo, poziția unghiului este de 0 grade coincide complet cu un unghi de 360 ​​de grade. Aceasta înseamnă că sinusurile, cosinusurile, tangentele acestor unghiuri sunt exact aceleași. Am marcat unghiul de 360 ​​de grade pentru a completa cercul.

   Să presupunem că, într-un mediu dificil de stres al examenului unificat de stat, te-ai îndoit cumva... Cu ce ​​este egal sinusul de 0 grade? Pare zero... Dacă e o unitate?! Memoria mecanică este așa ceva. În condiții dure, îndoielile încep să roadă ...)

   Calm, doar calm!) Vă voi spune o tehnică practică care vă va oferi un răspuns 100% corect și vă va îndepărta complet toate îndoielile.

   De exemplu, să ne dăm seama cum să determinăm clar și fiabil, să zicem, un sinus de 0 grade. Și, în același timp, cosinus 0. În aceste valori, destul de ciudat, oamenii se confundă adesea.

   Pentru a face acest lucru, desenați pe un cerc arbitrar colţ X. In primul trimestru, ca sa nu fie departe de 0 grade. Notați pe axe sinusul și cosinusul acestui unghi X, totul este chinezesc. Ca aceasta:

   Și acum - atenție! Reduceți unghiul X, aduceți partea mobilă spre axă OH. Plasați cursorul peste imagine (sau atingeți imaginea de pe tabletă) și vedeți totul.

   Acum porniți logica elementară!. Priviți și gândiți-vă: Cum se comportă sinx când unghiul x scade? Pe măsură ce unghiul se apropie de zero? Se micsoreaza! Și cosx - crește! Rămâne să ne dăm seama ce se va întâmpla cu sinusul când unghiul se prăbușește complet? Când se va așeza partea mobilă a unghiului (punctul A) pe axa OX și unghiul va deveni egal cu zero? Evident, sinusul unghiului va merge și el la zero. Și cosinusul va crește la ... la ... Care este lungimea laturii în mișcare a unghiului (raza cercului trigonometric)? Unitate!

   Iată răspunsul. Sinusul de 0 grade este 0. Cosinusul de 0 grade este 1. Absolut de fier și fără nicio îndoială!) Pur și simplu pentru că altfel nu poate fi.

   Exact în același mod, puteți afla (sau clarifica) sinusul de 270 de grade, de exemplu. Sau cosinus 180. Desenați un cerc, arbitrar un unghi într-un sfert de lângă axa de coordonate care ne interesează, mișcă mental latura unghiului și prinde ceea ce vor deveni sinusul și cosinusul când latura unghiului se așează pe axă. Asta e tot.

   După cum puteți vedea, nu este nevoie să memorați nimic pentru acest grup de unghiuri. nu este nevoie aici masa de sinus... da si masa cosinus- de asemenea.) Apropo, după mai multe aplicații ale cercului trigonometric, toate aceste valori sunt reținute de la sine. Și dacă sunt uitate, am desenat un cerc în 5 secunde și l-am clarificat. Mult mai ușor decât să suni un prieten de la toaletă cu riscul unui certificat, nu?)

   În ceea ce privește tangenta și cotangenta, totul este la fel. Desenăm o linie de tangentă (cotangentă) pe cerc - și totul este imediat vizibil. Unde sunt egale cu zero și unde nu există. Ce, nu știi despre liniile tangentei și cotangentei? Acest lucru este trist, dar se poate repara.) Am vizitat Secțiunea 555 Tangentă și cotangentă pe un cerc trigonometric - și nicio problemă!

   Dacă înțelegeți cum să definiți clar sinusul, cosinusul, tangenta și cotangenta pentru aceste cinci unghiuri - felicitări! Pentru orice eventualitate, vă informez că acum puteți defini funcții orice unghiuri care cad pe axă.Și acesta este 450°, și 540° și 1800°, și chiar un număr infinit ...) Am numărat (corect!) Unghiul pe cerc - și nu există probleme cu funcțiile.

   Dar, doar cu numărarea unghiurilor, apar probleme și erori... Cum să le evitați este scris în lecția: Cum să desenați (numărați) orice unghi pe un cerc trigonometric în grade. Elementar, dar foarte util în lupta împotriva erorilor.)

   Și iată lecția: Cum să desenezi (numărați) orice unghi pe un cerc trigonometric în radiani - va fi mai brusc. În ceea ce privește posibilitățile. Să presupunem că determinăm pe care dintre cele patru semiaxe se încadrează unghiul

   poți în câteva secunde. Nu glumesc! Doar în câteva secunde. Ei bine, desigur, nu numai 345 "pi" ...) Și 121, și 16 și -1345. Orice coeficient întreg este bun pentru un răspuns instantaneu.

   Ce se întâmplă dacă unghiul

   Gândi! Raspunsul corect se obtine in 10 secunde.Pentru orice valoare fractionara de radiani cu numitorul doi.

   De fapt, pentru asta este bun cercul trigonometric. Faptul că abilitatea de a lucra cu niste colțurile la care se extinde automat set infinit colțuri.

   Deci, cu cinci colțuri din șaptesprezece - mi-am dat seama.

   Al doilea grup de unghiuri.

   Următorul grup de unghiuri sunt unghiurile de 30°, 45° și 60°. De ce acestea, și nu, de exemplu, 20, 50 și 80? Da, cumva s-a întâmplat așa... Istoric.) Mai departe se va vedea cât de bune sunt aceste unghiuri.

   Tabelul de sinusuri, cosinus, tangente, cotangente pentru aceste unghiuri arată astfel:

   Unghiul x (în grade)	0	30	45	60	90
   Unghiul x (în radiani)	0
   sin x	0				1
   cos x	1				0
   tg x	0		1		nu substantiv
   ctg x	nu substantiv		1		0

   Am lăsat valorile pentru 0° și 90° din tabelul anterior pentru a fi complet.) Pentru a clarifica faptul că aceste unghiuri se află în primul cadran și cresc. De la 0 la 90. Acest lucru ne va fi util în continuare.

   Valorile din tabel pentru unghiurile 30°, 45° și 60° trebuie memorate. Zgârie dacă vrei. Dar și aici există o oportunitate de a vă face viața mai ușoară.) Acordați atenție valorile tabelului sinus aceste colturi. Si compara cu valorile tabelului cosinus...

   Da! Sunt la fel! Doar în ordine inversă. Unghiurile cresc (0, 30, 45, 60, 90) - iar valorile sinusului crește de la 0 la 1. Puteți verifica cu un calculator. Și valorile cosinusului - scădea de la 1 la zero. Mai mult decât atât, valorile înseși la fel. Pentru unghiuri de 20, 50, 80 acest lucru nu s-ar fi întâmplat...

   De aici o concluzie utilă. Suficient pentru a învăța Trei valori pentru unghiuri de 30, 45, 60 de grade. Și amintiți-vă că acestea cresc în sinus și scad în cosinus. Spre sinus.) La jumătatea drumului (45°) se întâlnesc, adică sinusul de 45 de grade este egal cu cosinusul de 45 de grade. Și apoi diverg din nou... Se pot învăța trei semnificații, nu?

   Cu tangente - cotangente, imaginea este exclusiv aceeași. Unu la unu. Doar valorile sunt diferite. Aceste valori (încă trei!) trebuie și ele învățate.

   Ei bine, aproape toată memorarea s-a terminat. Ați înțeles (sperăm) cum să determinați valorile pentru cele cinci unghiuri care cad pe axă și ați învățat valorile pentru unghiurile de 30, 45, 60 de grade. Total 8.

   Rămâne să ne ocupăm de ultimul grup de 9 cornere.

   Acestea sunt colturile:
   120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Pentru aceste unghiuri, trebuie să cunoașteți tabelul de fier al sinusurilor, tabelul cosinusurilor etc.

   Coșmar, nu?)

   Și dacă adăugați unghiuri aici, cum ar fi: 405 °, 600 ° sau 3000 ° și multe, multe dintre ele frumoase?)

   Sau unghiuri în radiani? De exemplu, despre colțuri:

   

   și multe altele ar trebui să știi toate.

   Cel mai amuzant lucru este să știi toate - imposibil în principiu. Dacă utilizați memoria mecanică.

   Și este foarte ușor, de fapt elementar - dacă folosești un cerc trigonometric. Dacă vă familiarizați cu cercul trigonometric, toate acele unghiuri îngrozitoare în grade pot fi ușor și elegant reduse la cele vechi bune:

   Apropo, mai am câteva site-uri interesante pentru tine.)

   Puteți exersa rezolvarea exemplelor și puteți afla nivelul dvs. Testare cu verificare instantanee. Învățarea - cu interes!)

   vă puteți familiariza cu funcțiile și derivatele.

   Trigonometria, ca știință, își are originea în Orientul Antic. Primele rapoarte trigonometrice au fost dezvoltate de astronomi pentru a crea un calendar precis și o orientare a stelelor. Aceste calcule s-au referit la trigonometria sferică, în timp ce la cursul școlar se studiază raportul dintre laturile și unghiul unui triunghi plat.

   Trigonometria este o ramură a matematicii care se ocupă cu proprietățile funcțiilor trigonometrice și cu relația dintre laturile și unghiurile triunghiurilor.

   În perioada de glorie a culturii și științei din mileniul I d.Hr., cunoștințele s-au răspândit din Orientul Antic până în Grecia. Dar principalele descoperiri ale trigonometriei sunt meritul oamenilor din Califatul Arab. În special, omul de știință turkmen al-Marazvi a introdus funcții precum tangenta și cotangenta, a compilat primele tabele de valori pentru sinusuri, tangente și cotangente. Conceptul de sinus și cosinus a fost introdus de oamenii de știință indieni. O mare atenție este dedicată trigonometriei în lucrările unor figuri atât de mari ale antichității precum Euclid, Arhimede și Eratostene.

   Mărimi de bază ale trigonometriei

   Funcțiile trigonometrice de bază ale unui argument numeric sunt sinus, cosinus, tangentă și cotangentă. Fiecare dintre ele are propriul grafic: sinus, cosinus, tangent și cotangent.

   Formulele pentru calcularea valorilor acestor mărimi se bazează pe teorema lui Pitagora. Este mai bine cunoscut școlarilor în formula: „Pantaloni pitagoreici, egali în toate direcțiile”, deoarece dovada este dată pe exemplul unui triunghi dreptunghic isoscel.

   Sinusul, cosinusul și alte dependențe stabilesc o relație între unghiurile ascuțite și laturile oricărui triunghi dreptunghic. Oferim formule pentru calcularea acestor mărimi pentru unghiul A și urmărim relația funcțiilor trigonometrice:

   

   După cum puteți vedea, tg și ctg sunt funcții inverse. Dacă reprezentăm catetul a ca produsul dintre sin A și ipotenuza c și catetul b ca cos A * c, atunci obținem următoarele formule pentru tangentă și cotangentă:

   

   cerc trigonometric

   Grafic, raportul cantităților menționate poate fi reprezentat astfel:

   

   Cercul, în acest caz, este tot valori posibile unghiul α — de la 0° la 360°. După cum se poate observa din figură, fiecare funcție ia o valoare negativă sau pozitivă în funcție de unghi. De exemplu, sin α va avea semnul „+” dacă α aparține sferturilor I și II ale cercului, adică se află în intervalul de la 0 ° la 180 °. Cu α de la 180° la 360° (sferturile III și IV), sin α poate fi doar o valoare negativă.

   Să încercăm să construim tabele trigonometrice pentru anumite unghiuri și să aflăm semnificația cantităților.

   

   Valorile lui α egale cu 30°, 45°, 60°, 90°, 180° și așa mai departe se numesc cazuri speciale. Valorile funcțiilor trigonometrice pentru acestea sunt calculate și prezentate sub formă de tabele speciale.

   

   Aceste unghiuri nu au fost alese întâmplător. Denumirea π din tabele este pentru radiani. Rad este unghiul la care lungimea unui arc de cerc corespunde razei acestuia. Această valoare a fost introdus pentru a stabili o relație universală, la calculul în radiani, lungimea reală a razei în cm nu contează.

   

   Unghiurile din tabele pentru funcțiile trigonometrice corespund valorilor radianilor:

   

   Deci, nu este greu de ghicit că 2π este un cerc complet sau 360°.

   Proprietățile funcțiilor trigonometrice: sinus și cosinus

   Pentru a lua în considerare și a compara proprietățile de bază ale sinusului și cosinusului, tangentei și cotangentei, este necesar să le trasăm funcțiile. Acest lucru se poate face sub forma unei curbe situate într-un sistem de coordonate bidimensional.

   Luați în considerare un tabel comparativ de proprietăți pentru o undă sinusoidală și o undă cosinus:

   

   sinusoid	unde cosinus
   y = sin x	y = cos x
   ODZ [-1; unu]	ODZ [-1; unu]
   sin x = 0, pentru x = πk, unde k ϵ Z	cos x = 0, pentru x = π/2 + πk, unde k ϵ Z
   sin x = 1, pentru x = π/2 + 2πk, unde k ϵ Z	cos x = 1, pentru x = 2πk, unde k ϵ Z
   sin x = - 1, la x = 3π/2 + 2πk, unde k ϵ Z	cos x = - 1, pentru x = π + 2πk, unde k ϵ Z
   sin (-x) = - sin x, adică funcție impară	cos (-x) = cos x, adică funcția este pară
   	funcția este periodică, cea mai mică perioadă este 2π
   sin x › 0, cu x aparținând sferturilor I și II sau de la 0° la 180° (2πk, π + 2πk)	cos x › 0, cu x aparținând sferturilor I și IV sau de la 270° la 90° (- π/2 + 2πk, π/2 + 2πk)
   sin x ‹ 0, cu x aparținând sferturilor III și IV sau de la 180° la 360° (π + 2πk, 2π + 2πk)	cos x ‹ 0, cu x aparținând sferturilor II și III sau de la 90° la 270° (π/2 + 2πk, 3π/2 + 2πk)
   crește pe intervalul [- π/2 + 2πk, π/2 + 2πk]	crește pe intervalul [-π + 2πk, 2πk]
   scade pe intervalele [ π/2 + 2πk, 3π/2 + 2πk]	scade pe intervale
   derivată (sin x)' = cos x	derivată (cos x)’ = - sin x

   Determinarea dacă o funcție este pară sau nu este foarte simplă. Este suficient să vă imaginați un cerc trigonometric cu semne de mărimi trigonometrice și să „pliați” mental graficul în raport cu axa OX. Dacă semnele sunt aceleași, funcția este pară; în caz contrar, este impară.

   

   Introducerea radianilor și enumerarea principalelor proprietăți ale undei sinusoide și cosinus ne permit să aducem următorul model:

   

   Este foarte ușor să verificați corectitudinea formulei. De exemplu, pentru x = π/2, sinusul este egal cu 1, la fel și cosinusul lui x = 0. Verificarea se poate face prin examinarea tabelelor sau prin trasarea curbelor funcției pentru valori date.

   Proprietățile tangentoidului și cotangentoidului

   Graficele funcțiilor tangente și cotangente diferă semnificativ de unda sinusoidă și cosinus. Valorile tg și ctg sunt inverse una față de cealaltă.

   

   

   1. Y = tgx.
   2. Tangenta tinde spre valorile lui y la x = π/2 + πk, dar nu le atinge niciodată.
   3. Cea mai mică perioadă pozitivă a tangentoidului este π.
   4. Tg (- x) \u003d - tg x, adică funcția este impară.
   5. Tg x = 0, pentru x = πk.
   6. Funcția este în creștere.
   7. Tg x › 0, pentru x ϵ (πk, π/2 + πk).
   8. Tg x ‹ 0, pentru x ϵ (— π/2 + πk, πk).
   9. Derivată (tg x)' = 1/cos 2 ⁡x .

   Luați în considerare reprezentarea grafică a cotangentoidului de mai jos în text.

   

   Principalele proprietăți ale cotangentoidului:

   1. Y = ctgx.
   2. Spre deosebire de funcțiile sinus și cosinus, în tangentoidul Y poate prelua valorile mulțimii tuturor numerelor reale.
   3. Cotangentoidul tinde spre valorile lui y la x = πk, dar nu le atinge niciodată.
   4. Cea mai mică perioadă pozitivă a cotangentoidului este π.
   5. Ctg (- x) \u003d - ctg x, adică funcția este impară.
   6. Ctg x = 0, pentru x = π/2 + πk.
   7. Funcția este în scădere.
   8. Ctg x › 0, pentru x ϵ (πk, π/2 + πk).
   9. Ctg x ‹ 0, pentru x ϵ (π/2 + πk, πk).
   10. Derivată (ctg x)' = - 1/sin 2 ⁡x Fix